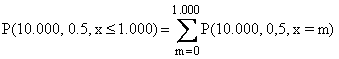6
PROBABILÍSTICA Y LAS
FORMAS
DE TRANSICIÓN INEXISTENTES
por DAVID J.
RODABAUGH, Ph. D.
Se documenta
fácilmente con los escritos de los mismos evolucionistas que no existe evidencia
fósil de formas de transición. El propósito de este artículo es calcular la
probabilidad de este fenómeno si se asume que tuvo lugar una evolución por medio
de micromutaciones. La conclusión es que las formas de transición nunca han
existido.
INTRODUCCIÓN
Por «evolución» se significa la
teoría de evolución «desde las moléculas al
hombre». El término «forma de
transición» se utiliza de aquellas supuestas formas que
hubieran sido a la vez intermedias y antecesoras. El que tales formas
están virtualmente ausentes del registro fósil (tal como
se ha descubierto) ha sido admitido por George G. Simpson, que
afirmó:
«...las secuencias
continuas de transición no es que sean raras solamente, sino que son
virtualmente inexistentes... Su ausencia es tan universal que no se puede
atribuir, apresuradamente, de una manera total a la casualidad, y sí que exige
algún intento de explicación, como la mayor parte de los paleontólogos
sienten.»
Y Simpson ha
admitido que en ningún lugar existe ni trazas de un fósil que cierre la
discontinuidad entre el caballo y cualquier presumible antecesor, y además ha
afirmado:
«Esto es cierto de
todos los treinta y dos órdenes de mamíferos. ...Los miembros más tempranos y
primitivos conocidos de cada orden ya presentan todas sus características
ordinales básicas y en ningún caso existe ninguna secuencia conocida
aproximadamente continua de uno a otro. En muchos casos la discontinuidad es tan
brusca y tan grande que el origen del orden es especulativo y muy discutido.»
Además, D. M.
Raup y S. M. Stanley afirmaron, en 1971:
«Desafortunadamente, el origen de la mayor parte de las categorías
altas está cubierto de misterio; generalmente las nuevas categorías altas
aparecen bruscamente en el registro fósil sin evidencia de formas de
transición.»
Que la
ausencia de formas de transición en el registro fósil, por todo lo que se conoce
del mismo, no se pueda atribuir enteramente a la casualidad lo admite Simpson
decididamente en la primera cita. Este artículo demostrará una afirmación aún
más rotunda utilizando ideas bien conocidas de la probabilística. La
consecuencia es que nunca existieron tales formas de transición.
El lector debe
entonces concluir o bien que el evolucionismo tuvo lugar por medio de
macromutaciones (el concepto de «hopeful monster» o «monstruo viable») o bien
que el evolucionismo es falso. Los evolucionistas han rechazado, por lo general,
la idea del «monstruo viable» porque ni siquiera ellos pueden imaginarse cómo
podría suceder una cosa así. En tanto que se han observado micromutaciones, no
se ha observado ninguna macromutación que no destruyera al organismo. Por ello
la macromutación no constituye ninguna explicación.
1.
Distribuciones
La situación
básica es la siguiente: Supongamos que existe una probabilidad de p de
que cuando se descubra un fósil éste sea de transición. Supongamos también que
se descubren n fósiles y que k de ellos son de transición. Se
pueden plantear dos cuestiones. Primero, ¿cuál es la probabilidad de este
suceso? Segundo, ¿cuál es la probabilidad dados n, p y k, de que m
de los fósiles sean de transición para m ≤ k?
Estas
cuestiones se pueden formalizar con ayuda de algunas notaciones.
Definiciones: Definamos P(n, p, x
= k) como la probabilidad de que haya exactamente k
consecuciones en n intentos en los que cada consecución tiene una
probabilidad p. Definamos P(n, p, x ≤ k) como la
probabilidad de k o menos consecuciones en n intentos en los que
cada consecución tiene una probabilidad p.
Las dos
cuestiones anteriores se reducen a los problemas de calcular P(n, p, x = k)
y P(n, p, x ≤ k). Si x ≤ k, entonces x = 0, ó x = 1 ó ... ó x = k. De
ello sigue lo siguiente:
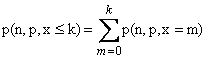 (1)
(1)
Para ilustrar
lo anterior, consideremos el sencillo problema de echar una moneda a cara o
cruz. Para cada intento, la probabilidad de que caiga de cara es 1/2. La
probabilidad de tirar tres veces una moneda y conseguir cara las tres veces es
de (1/2)3, o 1/8. Esto es, P(3, 1/2, x = 3) = 1/8 en esta situación.
No obstante, siempre sucede que si se echa una moneda al aire tres veces, no
puede dar cara más que tres veces como máximo. Esto es, P(3, 1/2, x ≤ 3) =
1.
La situación
descrita anteriormente es la del Ensayo de Bernouilli. Se define de la
manera siguiente: Si la probabilidad de éxito es la misma para cada uno de
los n intentos, se dice que los intentos son independientes. Los intentos
repetidos que cumplen estas condiciones reciben el nombre de Ensayos de
Bernouilli.
La
probabilidad de exactamente k consecuciones en n intentos
independientes de este tipo es de :
 (2)
(2)
donde
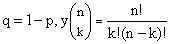
Debido al
hecho de que el lado derecho de la ecuación procede de la expansión binomial de
(p + q)n, la distribución determinada por la ecuación (2) recibe el
nombre de distribución binómica.
La sustitución
de la ecuación (2) en la ecuación (1) nos da
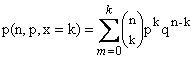 (3)
(3)
Consideremos
ahora el problema de la probabilidad de que el siguiente fósil descubierto fuera
transicional.
Sea t
el número de formas transicionales (con respecto a unas ciertas características
o en general), y sea N el número de organismos que no son transicionales.
Por ejemplo, si la característica bajo estudio es la de ser un ave, entonces
N es el número de aves y t es el numero de organismos de
transición (poseyendo alas parciales). La probabilidad de que el primer fósil
sea transicional es
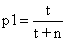 (4)
(4)
Naturalmente,
no existe ninguna razón por la cual una forma de transición no vaya a ser
fosilizada menos que una forma no de transición.
Habiendo
extraído el primer fósil, la probabilidad de que el segundo fósil sea de
transición es
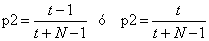
 (5)
(5)
dependiendo de si
la primera era de transición o no.
Este es,
técnicamente, el problema de muestrear sin reemplazar, y la distribución
binómica no representa exactamente las probabilidades, ya que p 1
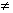 p2
p2 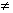 p3 ...
p3 ... 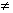 pn.
pn.
Un ejemplo nos
podrá ser de utilidad. Supongamos una bolsa conteniendo 30 bolas idénticas
excepto por el color. Supongamos además que 10 bolas son de color negro y que 20
son blancas. La probabilidad de extraer una bola negra al primer intento es de
10/30, o de 1/3. Esta es la situación representada por la distribución
binómica.
No obstante,
si no se reintroduce la primera bola extraída, entonces la probabilidad de que
la segunda bola sea negra ya no es 1/3, es 9/29 si la primera hubiera sido negra
y 10/29 si hubiera sido blanca. La distribución hipergeométrica representa esta
situación.
No obstante,
cuando el número total es muy grande, aunque el muestreo sea sin
reemplazamiento, se puede utilizar la distribución binómica como aproximación. En el estudio de los
hallazgos fósiles el número total de organismos N + t está por lo
menos en el orden de los miles de millones, por lo que la distribución binómica
representada por la ecuación (2) y por la ecuación (3) es una aproximación
excelente.
Otra
distribución útil en este tipo de problema es la distribución de probabilidad de
Poisson definida por
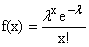 (6)
(6)
Cuando
p es pequeño y n es grande la función de Poisson se aproxima a la
binómica. En este caso tenemos l = np y
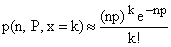 (7)
(7)
(Se utiliza la
notación ≈ para indicar aproximación.)
Sustituyendo
(7) en (1) obtenemos
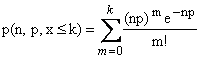 (8)
(8)
2. Algunos
valores razonables para n y p
El resto de
este artículo trata de la aplicación de las distribuciones binómica y de Poisson
para hallar P(n, p, x = k) y P(n, p, x ≤ k) donde n
es el número de fósiles descubiertos, p es la relación t/t + EN
que es la probabilidad de hallar una forma de transición, y k es el
número de formas de transición descubiertas.
(Recordamos al
lector que, en este artículo, forma de transición significa a la vez intermedia
y antecesora).
Es bastante
difícil conseguir información fiable sobre el número total de fósiles
descubiertos o incluso del número total en categorías particulares:
No obstante,
Pierce Brodkorb afirma que existen 1.760 especies de aves fósiles. Aceptando un promedio de
seis fósiles por especie, ello implica unos 10.000 fósiles de aves, todos los
cuales son completamente alados y poseen plumas. Pero hasta el presente no se ha
hallado un solo fósil con alas solamente parcialmente desarrolladas. Así, para
una característica muy especial (no poseída por muchos organismos), 10.000 es
una cifra muy moderada para n.
En realidad,
para la propiedad del vuelo queda justificada una cifra mucho más grande. Ello
se debe a que existen muchos insectos voladores, así como quirópteros y reptiles
voladores.
Otras
características dignas de investigación son los ojos, pulmones, reproducción
sexual, etc. Además, existe el problema de la evidencia, que se admite no
existe, de formas de transición entre cada uno de los 32 órdenes de mamíferos y
sus supuestos antecesores, mencionado ello por Simpson.
Así, es más
razonable suponer n = 100.000 ó n = 1000.000.
En este
articulo se calculan las probabilidades para n = 10.000, n =
100.000 y n = 1.000.000. En realidad hay suficiente justificación para utilizar
valores mayores, pero, como verá el lector, la situación resultante del examen
de estas cifras es suficiente para echar por tierra toda posible credibilidad de
las afirmaciones evolucionistas con respecto al registro fósil.
¿Cuál será el
valor razonable de p? La teoría estándar de la evolución es que las
micromutaciones (pequeños cambios) dan razón de toda la variación observable.
Así, el número de especies de transición tiene que ser realmente
grande.
En realidad,
para poder dar cuenta de la aparición de las aves por medio del supuesto proceso
de micromutaciones se precisaría postular un vasto número de especies que fuesen
a la vez intermedias y antecesoras. Además, cada especie debe ser razonablemente
viable a fin de dar el tiempo suficiente a que dé origen a algún descendiente
«evolucionado». Por lo tanto, sería de esperar que, basándonos solamente en
la teoría evolucionista, p ≥ 0,9.
No obstante,
los cálculos aquí expuestos se basarán en cifras mucho más favorables para los
evolucionistas. Se calculará la función P(n, p, x ≤ k) para
p = 0,5; 0,1; 0,01. Se recuerda al lector que p = 0,01 implica que
solamente hubiera existido un organismo de transición por cada 99
organismos no transicionales –cosa totalmente contraria a las predicciones
basadas en el modelo evolucionista. Pero incluso esto, como se verá, conduce a
quebraderos de cabeza para los evolucionistas.
Antes de
finalizar esta sección, se debería comentar sobre los valores de k. A
pesar de que no se han hallado formas de transición hasta el
presente, se calcularán las probabilidades en base de k = 0, 5 y
10.
Para
sumarizar, P(n, p, x ≤ k) se calculará para n = 10.000; 100.000;
1.000.000; p = 0,5; 0,1; 0,01; k = 0; 5; 10. También se
calculará P(n, p, x = k) en algunos casos.
3.
Dificultades de cálculo
Se puede
utilizar una computadora moderna digital de alta velocidad (como IBM 360 ó IBM
370) para trabajar con números distintos de cero y con valores absolutos dentro
del margen
16–64 ≤ x ≤
1663
(9)
El campo de un
calculador electrónico Hewlett-Packard (así como el de otros) es
10–99 ≤ x <
10100
(10)
Este campo es
suficiente para la mayor parte de propósitos. No obstante, lo que sigue se puede
verificar rápidamente utilizando logaritmos (todos los que se utilizan en este
artículo son de base 10):
p(10.000, 0.5, x = 10) = 10–2976,862
(11)
Si todo lo que
se deseara fuese P(n, p, x = k), se podrían calcular fácilmente
las ecuaciones (7) y (2) utilizando logaritmos.
Desafortunadamente, tanto para k = 5 y k = 10 es
necesario calcular las ecuaciones (3) y (8), cada una de las cuales es una suma
de términos demasiado pequeños para poderlos representar en cualquier
computadora o calculadora conocida. El problema consiste en evaluar la
suma
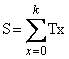 (12)
(12)
en la que
algunos, o quizá todos, de los términos Tx no son representables ni en la
calculadora ni en la computadora. Se puede entonces reescribir la ecuación (12)
como
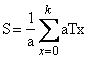 (13)
(13)
Entonces, sin
importar cual sea el valor de S, se puede hallar una a con la que
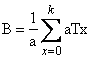 (14)
(14)
sea representable
en la máquina. El valor de log S se puede entonces hallar de la siguiente
manera:
log S = log B – log
a
(15)
ya que aS =
B.
Además, el
logaritmo de cada término aTx puede calcularse utilizando logaritmos, y se puede
convertir al valor aTx antes de añadirse a las sumas parciales de B.
El proceso
anterior fue empleado en una calculadora Hewlett-Packard 25 programable a fin de
obtener los valores que se muestran en la siguiente sección.
4.
Aplicaciones
En esta
sección se tabulan los valores P(n, p, x ≤ k) en base de los valores indicados
en la sección 2. Estos resultados son tan pequeños que es necesario dar tan solo
los logaritmos en las tablas.
Aunque la
distribución de Poisson es tan solo una aproximación, los valores basados en
ella se muestran en la tabla 2.
El lector
descubrirá que cuando p = 0,01 los valores de las dos tablas difieren muy
poco.
Se recordará
que cuando el logaritmo es, por ejemplo, –4557,60, el número es
10–4557,60, alrededor de 2,5 x 10–4558. En este caso 1a
probabilidad vendría indicada por un número decimal con 4.557 ceros después de
la coma decimal, y después un dos. Desde luego, éste es un número lo suficiente
pequeño como para convencer a cualquiera.
5.
Conclusiones
Emil Borel, el
famoso matemático, dijo:
«Podemos entonces
ser guiados a tomar 10
–50 como el valor de probabilidades
despreciables a escala cósmica. Cuando la probabilidad de un suceso está por
debajo de este límite, se puede esperar con toda certeza que lo que ocurrirá
será el suceso opuesto, cualquiera que sea el número de ocasiones que se
presenten en el universo entero.»
En otro libro
afirmó: «Los sucesos cuya probabilidad es muy pequeña nunca tienen lugar.»
Sea E
el suceso descrito como sigue: Supongamos que se descubren n fósiles,
y que no más de k son de transición (o sea, k o una cantidad
inferior). Supongamos además que el número de formas de transición dividido por
el número total de organismos es p.
Ahora, la
probabilidad de E, denotada por π(E) viene dada por
π(E) = P(n, p, x ≤
k)
(16)
Hasta la
fecha, el valor es k = 0. O sea, no existen criaturas parcialmente aladas,
etc. No obstante, para seguir la discusión, hagamos que k = 5 ó k =
10.
Una
consecuencia de las dos tablas y de las afirmaciones de Borel es que E no
puede tener lugar.
De hecho, si
n = 10.000, entonces
Log P(10.000, 0.5, x = 1.000) =
–1040,11
(17)
ahora,
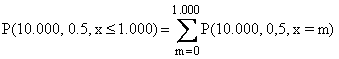
(1.000) p(10.000, 0,5, x =
1000)
(18)
Así,
Log p(10.000, 0,5, x ≤ 1000)
< Log(1.000) + Log
P(10.000, 0,5, x = 1.000) =
3 – 10 40,11 = –1037,11
(19)
Ni siquiera
este suceso es posible. Uno es llevado pues a la conclusión inevitable de que,
si hubo formas de transición, fueron extremadamente escasas. Por lo tanto, una
de dos, o el mundo biológico actual vino a ser como es por macromutaciones
(«monstruos viables»), o por creación especifica.
Ya que el
concepto de «monstruo viable» es rechazado por casi todos los evolucionistas, la
mente sin prejuicios tiene que llegar a la conclusión de que la creación
específica es el único modelo que concuerda con los hechos.
Otra
observación que se debe hacer es que las cifras presentadas en este artículo
hacen que las cifras en un artículo reciente sean demasiado amables con los
evolucionistas.13 Las probabilidades P(n, p, x ≤ k)
deberían tomar el lugar de P(G/E) en aquel artículo.
TABLAS
TABLA 1. Log P(n, p, x ≤ k)
basada en DISTRIBUCIÓN BINÓMICA
|
P |
n = 10.000 |
n = 100.000 |
n =
1.000.000 |
|
0,5 |
–3010,30 |
–30103,00 |
–301030,00 |
|
k
= 0 0,1 |
–457,57 |
–4575,75 |
–45757,49 |
|
0,01 |
–43,65 |
–436,48 |
–4364,81 |
|
0,5 |
–2992,38 |
–30080,08 |
–301002,07 |
|
k
= 5 0,1 |
––444,42 |
–4557,60 |
–45734,34 |
|
0,01 |
–35,68 |
–423,54 |
–4346,86 |
|
0,5 |
–2976,86 |
–30059,56 |
–300976,56 |
|
k
= 10 0,1 |
–433,68 |
–4541,85 |
–45713,59 |
|
0,01 |
–30,12 |
–412,99 |
–4331,32 |
TABLA 2. Log P(n, p, x ≤ k)
basada en la DISTRIBUCIÓN DE POISSON
|
P |
n = 10.000 |
n = 100.000 |
n = 1.000.000 |
|
0,5 |
–2172,47 |
–21714,72 |
–217147,24 |
|
k
= 0 0,1 |
–434,29 |
–4342,94 |
–43429,45 |
|
0,01 |
–43,43 |
–434,29 |
–4342,94 |
|
0,5 |
–2155,06 |
–21693,31 |
–217120,83 |
|
k
= 5 0,1 |
–421,37 |
–4325,02 |
–43406,53 |
|
0,01 |
–35,49 |
–421,37 |
–4325,02 |
|
0,5 |
–2141,04 |
–21674,29 |
–217086,81 |
|
k
= 10 0,1 |
–410,85 |
–4309,50 |
–43386,01 |
|
0,01 |
–29,94 |
–410,85 |
–4309,50 |
 Ir a la siguiente
sección del libro
Ir a la siguiente
sección del libro Volver al
Índice de Creación, Evolución y el Registro Fósil
Volver al
Índice de Creación, Evolución y el Registro Fósil Volver a libros Creación y
Ciencia
Volver a libros Creación y
Ciencia Volver a la
página principal
Volver a la
página principal Volver al índice general castellano
Volver al índice general castellano



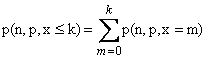 (1)
(1)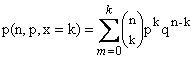 (3)
(3)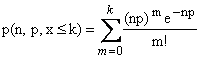 (8)
(8)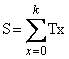 (12)
(12)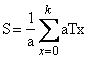 (13)
(13)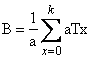 (14)
(14)